10 conseils gratuits pour devenir un champion en maths
Les nombres premiers
Le mot arithmétique vient du grec, et signifie nombre. L’arithmétique est une branche des mathématiques qui étudie les nombres. Parmi ces nombres, certains ont des propriétés bien particulières, c’est le cas des nombres premiers.
Les élèves sont initiés à l’arithmétique et aux nombres premiers dès le collège.
La découverte de ces nombres remonte à l’Antiquité. Euclide en donne la définition et prouve qu’il en existe une infinité 300 ans avant J.C.
Qu’est-ce qu’un nombre premier ?
Un nombre premier est un entier naturel non nul qui admet exactement deux diviseurs : 1 et lui-même. Par exemple : \quad 3 \div 1 = 3 \quad et \quad 3\div 3 = 1
3 n’est divisible que par 1 et 3 (lui-même). En effet, si l’on divise 3 par un autre nombre, on n’obtient pas un nombre entier.\quad 3 \div 2 = 1,5\quad ou \quad 3 \div 4 = 0,75 etc.
Puisque 3 n’admet que 2 diviseurs (1 et lui-même), alors 3 est un nombre premier
1 n’a qu’un seul diviseur, (lui-même) il n’est donc pas premier.
0 est divisible par tout nombre non nul, il a une infinité de diviseurs et 0 n’est pas un nombre premier.
Par conséquent, le plus petit nombre premier est 2
Qu’est-ce qu’un nombre composé ?
Un nombre composé est un entier naturel non nul qui admet plus de deux diviseurs , autrement dit un nombre est composé s’il est le produit d’au moins deux nombres premiers.
Exemple : 6 est un nombre composé car il possède 4 diviseurs: 1,2,3 et 6. On peut aussi constater que 6=3\times 2, donc 6 est le produit de deux nombres premiers
1 n’est pas un nombre composé car il n’a qu’un diviseur (lui-même). Et 0 non plus ! En effet pour qu’un produit soit nul, il faut qu’au moins un de ses facteurs soit nul. Or 0 n’est pas premier. Ainsi 0 n’est pas le produit de nombres premiers.
Comment déterminer tous les nombres premiers inférieurs à 100 ?
En décembre 2017, une équipe de chercheur a découvert un nouveau très grand nombre premier. Evidemment, ces mathématiciens disposent de très gros moyen.
Il existe cependant une méthode simple et rapide pour déterminer tous les nombres premiers plus petits que 100.
- Noter en ligne, les multiples de 6 inférieurs à 100
- Au-dessus, noter les nombres entiers précédents les multiples de 6
- Au-dessous, noter les nombres entiers suivants les multiples de 6
- Éliminer tous les multiple de 5, sauf 5 (nombres se terminant par 0 ou 5) soit : 25,35,55,65,85,95.
- Éliminer tous les multiple de 7, sauf 7 soit : 77,49 et 91 (91=7\times 13)
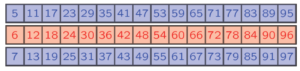
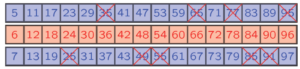
Tous les nombres en bleu (ligne du haut, et du bas) sont des nombres premiers. Attention, pour obtenir tous les nombres premiers inférieurs à 100, il ne faut pas oublier 2 et 3 !
