10 conseils gratuits pour devenir un champion en maths
Les triangles semblables
(définition et propriétés)
En géométrie plane, les triangles semblables font partie des connaissances bases à acquérir dès le collège.
Définition: Deux triangles sont semblables, si leurs angles sont égaux deux à deux.
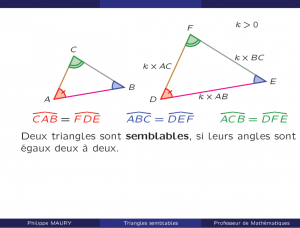
En pratique, il suffit de montrer que deux angles d’un triangle sont égaux à deux angles de l’autre triangle pour conclure qu’ils sont semblables.
En effet, la somme des mesures des angles d’un triangle est égale à 180 degrés. Par conséquent, si deux angles sont égaux deux à deux, le troisième l’est nécessairement.
Si deux triangles sont semblables, alors les longueurs des côtés de l’un sont proportionnelles aux longueurs des côtés de l’autre.
Réciproquement, si deux triangles ont les longueurs de leurs côtés proportionnelles, alors ils sont semblables.
Le coefficient de proportionnalité est en général noté k (k est un nombre réel strictement positif)
Par exemple si les triangles ABC et DEF sont semblables alors : DE=kAB, DF=kAC et EF=kBC et réciproquement si les longueurs des côtés des triangles ABC et DEF sont telles que DE=kAB, DF=kAC et EF=kBC alors ces triangles sont semblables.
De plus si k est strictement supérieur à 1 alors DE>AB, DF>AC et EF>BC ainsi le triangle DEF est un agrandissement du triangle ABC et si k est compris entre 0 et 1 alors DE<AB, DF<AC, EF. Enfin, si k est égal à 1 alors DE=AB, DF=AC et EF=BC et les triangles ABC et DEF sont identiques. On dit qu’ils sont isométriques ou superposables.
Puisque les longueurs des côtés des triangles ABC et DEF sont proportionnelles on a l’égalité des rapports :
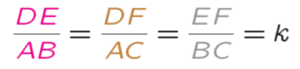
Pour retrouver facilement cette égalité, visualiser l’astuce présentée dans la vidéo.
