Il ne s’agit pas ici d’une démonstration mathématique de la formule pour calculer le volume des pyramides, mais d’une justification par une approche géométrique. Cette formule est un outil indispensable en maths, il convient de bien la comprendre pour la mémoriser aisément.
Volume des pyramides à base carrée
Considérons la pyramide à base carrée ci-dessous. Sa base est un carré de coté a. Dans un premier temps, pour simplifier, on considère que la hauteur de cette pyramide mesure a. De plus le pied de cette hauteur est un sommet du carré de base.
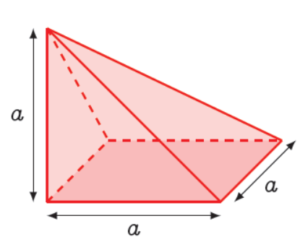
En dupliquant cette pyramide 2 fois on obtient 3 pyramides identiques que l’on peut agencer pour former un cube d’arête a
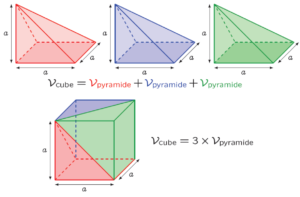
On visualise ainsi que le volume du cube est égal à 3 fois le volume d’une pyramide. Par conséquent, le volume de la pyramide vaut le tiers du volume du cube. \mathcal{V}_{\text{pyramide}}=\dfrac13\times \mathcal{V}_{\text{cube}}
Or, le volume du cube s’obtient en multipliant l’aire de sa base par sa hauteur, soit :
\mathcal{V}_{\text{cube}}=\mathcal{A}_{\text{base}} \times h =a^2 \times a = a^3
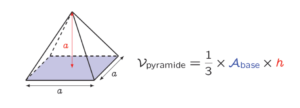
Ainsi le volume de la pyramide est : \mathcal{V}_{\text{pyramide}}=\dfrac13\times \mathcal{A}_{\text{base}}\times h
En déplaçant horizontalement le sommet, on obtient une nouvelle pyramide mais son volume est inchangé.
Volume des pyramides à base rectangulaire
On peut facilement reconduire le même raisonnement avec une pyramide dont la base est un rectangle de longueur L et de largeur \ell . la hauteur de cette pyramide mesure h. Comme précédemment le pied de cette hauteur est un sommet du rectangle de base.
Apres copie et agencement de ces pyramides on obtient un parallélépipède rectangle ou pavé droit de dimensions L \times \ell \times h
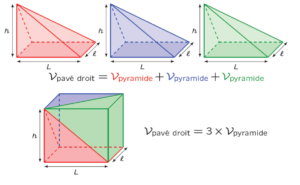
Ainsi, il est facile de vérifier que le volume du pavé droit est égal à 3 fois le volume d’une pyramide. Par conséquent, le volume d’une pyramide vaut le tiers du volume du pavé droit.
\mathcal{V}_{\text{pyramide}}=\dfrac13\times \mathcal{V}_{\text{pavé droit}}
Mais, le volume d’un pavé droit s’obtient en multipliant l’aire de sa base par sa hauteur, soit :
\mathcal{V}_{\text{pavé droit}}=\mathcal{A}_{\text{base}} \times h =L \times \ell \times h
On retrouve que le volume de la pyramide est : \mathcal{V}_{\text{pyramide}}=\dfrac13\times \mathcal{A}_{\text{base}}\times h
En déplaçant le sommet, on obtient une nouvelle pyramide mais son volume est toujours calculé avec la même formule.
Généralisation
On démontre que quelle que soit la forme de la base de la pyramide, son volume est toujours égal à \mathcal{V}_{\text{pyramide}}=\dfrac13\times \mathcal{A}_{\text{base}}\times h. Evidemment, il convient juste de calculer l’aire de la base en tenant compte de sa forme.
Si la base est un disque, alors on obtient un cône et son volume est donné par la même formule \mathcal{V}_{\text{cône}}=\dfrac13\times \mathcal{A}_{\text{base}}\times h
